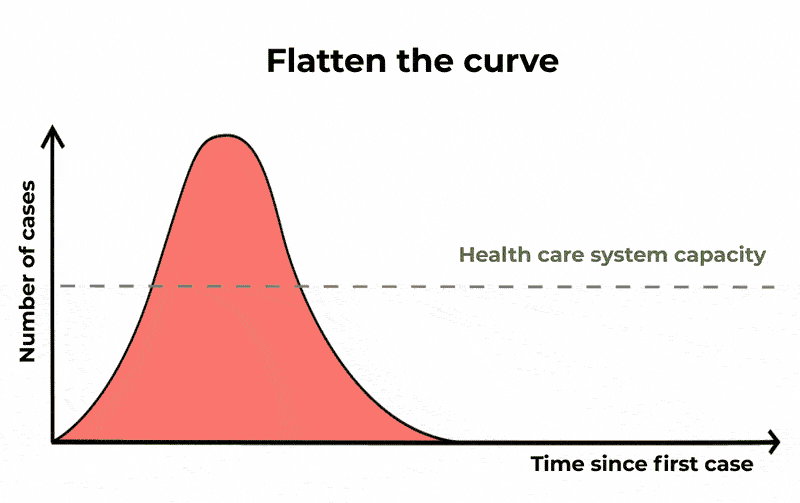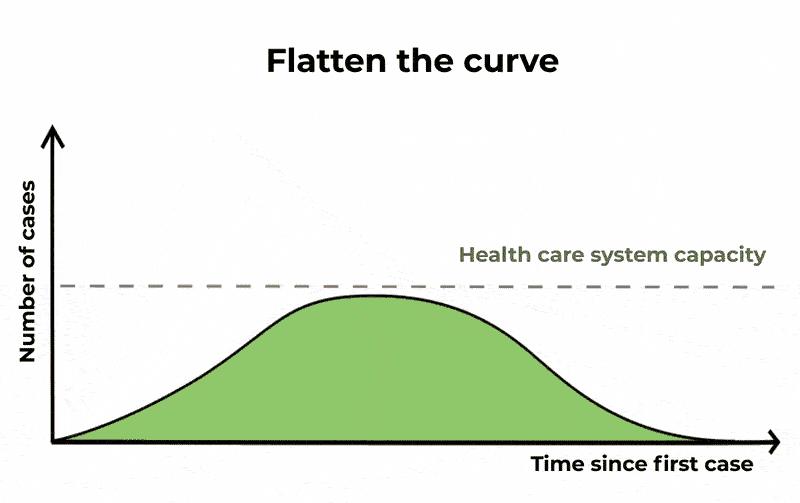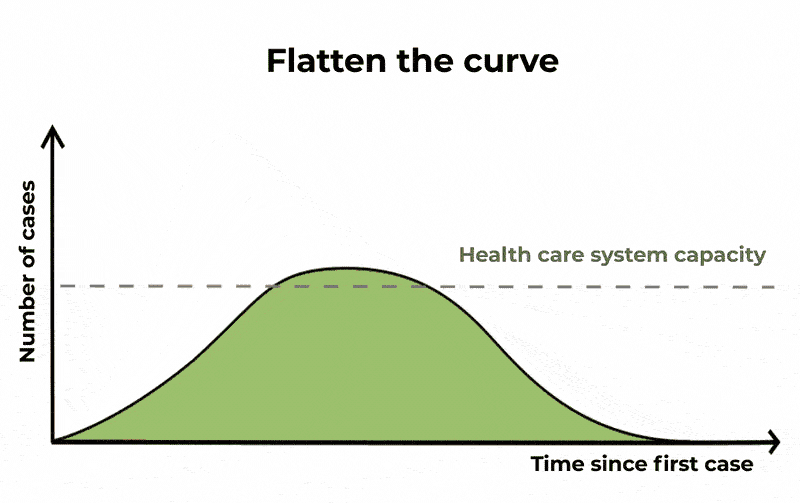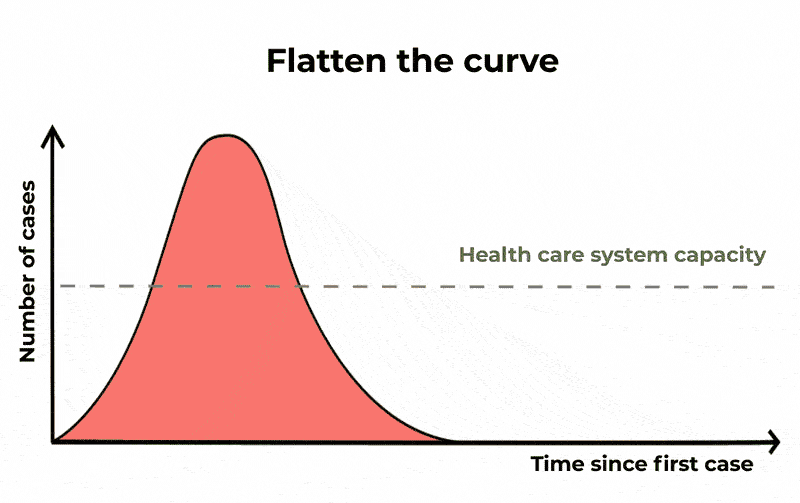
Dengan melakukan hal itu, jumlah orang yang terinfeksi mungkin akan sama, dan epidemi akan berlangsung lebih lama, tapi jumlah kasus yang parah akan menyebar. Ini berarti jika Anda memplot grafik jumlah kasus dari waktu ke waktu, pelonjakan dan penurunan kurva lebih lama terjadi tapi puncak kurva ini lebih rendah. Dengan “meratakan kurva” seperti ini, unit perawatan intensif akan lebih kecil kemungkinannya untuk kehabisan kapasitas.
Karena saat ini tidak ada vaksin atau obat khusus untuk menangani COVID-19, satu-satunya cara yang dapat dilakukan untuk mengurangi penyebaran virus adalah menjaga kebersihan agar tetap baik, mengisolasi orang-orang yang dicurigai terinfeksi, dan dengan melakukan langkah-langkah menjaga jarak sosial seperti membatalkan acara-acara besar dan menutup kegiatan sekolah.
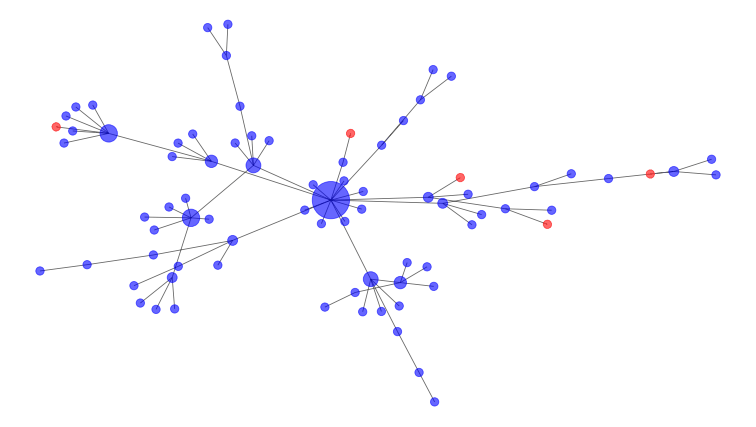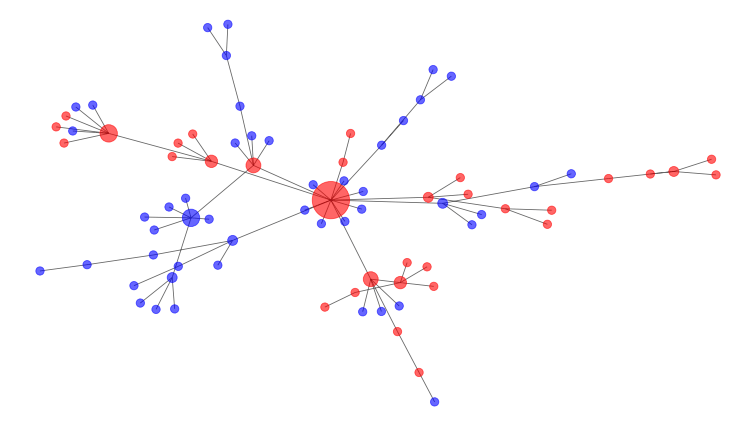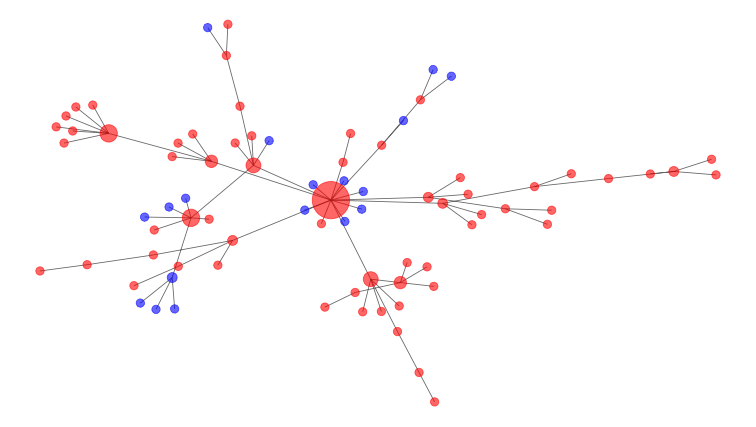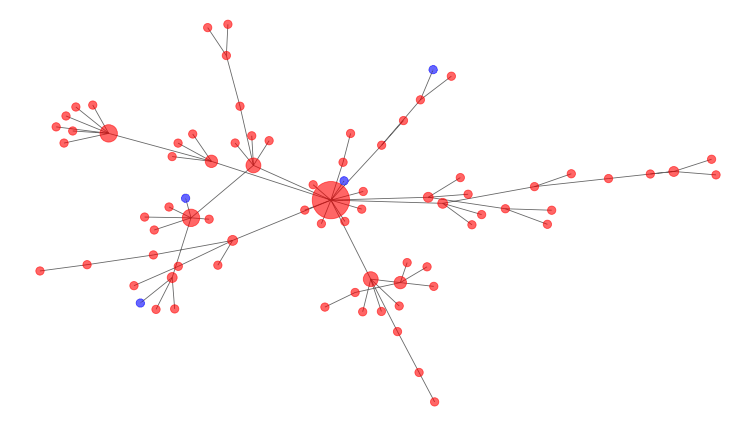
Situasi ini tentu saja tidak semudah proses percabangan sederhana. Beberapa orang dapat berinteraksi lebih banyak daripada yang lainnya dan mungkin melakukan kontak pula dengan berbagai kelompok (klaster) yang berbeda.
Matematikawan memodelkan hubungan-hubungan ini sebagai sebuah jaringan sosial, seperti contoh yang ditampilkan pada gambar di bawah. Orang yang terinfeksi direpresentasikan dengan simpul merah dan orang yang rentan tertular dengan simpul biru. Simpul besar yang berada di tengah diagram merupakan seorang penular ke banyak orang atau “super spreader”, seseorang yang melakukan kontak dengan banyak orang sehingga memiliki potensi yang lebih besar untuk menyebarkan penyakit.
Langkah-langkah intervensi membantu menghilangkan simpul dan memutus hubungan antarkedua kelompok tersebut.
Pada diagram di atas, simpul tengah yang sangat terhubung dengan simpul-simpul lainnya menjadi titik terbaik yang dihilangkan untuk menghindari koneksi berbagai kelompok. Itulah mengapa menghindari pertemuan publik yang besar selama wabah COVID-19 merupakan ide yang baik.
Simulasi matematis mengenai jaga jarak sosial telah menunjukkan bagaimana memecah jaringan secara terpisah membantu meratakan kurva infeksi penyakit.
Berapa banyak jarak sosial yang diperlukan untuk cukup meratakan kurva hingga menghindari kewalahan terjadi di rumah sakit? Apakah cukup dengan mengisolasi orang yang telah memiliki kontak dengan mereka yeng memiliki kasus positif? Apakah kita perlu penutupan acara-acara sosial, sekolah, dan tempat kerja secara luas?
Jawaban untuk pertanyaan-pertanyaan ini membutuhkan pemodelan matematika.
Kita masih dalam tahap awal wabah COVID-19 dan ada ketidakpastian besar tentang karakterisitik virus ini. Untuk memprediksi pertumbuhan COVID-19 secara akurat, dinamika penyebaran virus yang mendasarinya perlu ditentukan terlebih dulu.
Beberapa faktor yang mendorong penyebaran virus di antaranya:
Baca Juga: Masker Bedah Langka, Ganti dengan Masker Kain yang Juga Efektif Tangkal Virus
Karena data tersebut dikumpulkan dan diintegrasikan ke dalam model selama beberapa bulan mendatang, kami tentu akan memperlihatkan dengan lebih baik prediksi yang akurat dari jalur pertumbuhan COVID-19.
Sampai saat itu tiba, lebih baik berbuat salah karena kehati-hatian dan mengambil tindakan cepat untuk memperlambat penularan, daripada mengambil risiko dengan tidak melakukan dan membuat lonjakan kasus yang besar sehingga membuat sistem kesehatan kita mengalami ancaman yang serius.
Penulis: Andrew Black, Lecturer in Applied Mathematics, University of Adelaide; Dennis Liu, PhD Candidate, University of Adelaide, dan Lewis Mitchell, Senior Lecturer in Applied Mathematics, University of Adelaide
Artikel ini terbit pertama kali di The Conversation. Baca artikel sumber.
| Source | : | The Conversation Indonesia |
| Penulis | : | National Geographic Indonesia |
| Editor | : | Gita Laras Widyaningrum |

KOMENTAR